Cara menentukan himpunan penyelesaian pertidaksamaan kuadrat diawali dengan menentukan akar-akar pertidaksamaan kuadrat. Cara menentukan akar-akar pertidaksamaan kuadrat masih sama dengan cara menentukan akar-akar persamaan kuadrat. Hanya saja diperlukan langkah dengan mengambil harga nol nya. Untuk metode yang digunakan untuk menentukan akar-akar persamaan kuadrat bisa menggunakan metode pemfaktoran, menggunakan rumus abc, atau metode melengkapkan kuadrat sempurna. Setelah mendapatkan akar-akar persamaan kuadrat, langkah berikutnya adalah menggambar garis bilangan yang sesuai dan menentukan titik uji. Titik uji digunakan untuk menentukan daerah pada garis bilangan tersebut, apakah positif atau negatif. Setelah mendapatkan daerahnya, langkah berikutnya adalah menentukan himpunan penyelesaian pertidaksamaan yang diberikan.
Secara ringkas, cara menentukan himpunan penyelesaian pertidaksamaan kuadrat dapat dilihat melalui ringkasan pada daftar di gambar berikut.

Bentuk Umum Pertidaksamaan Kuadrat
Sama seperti pada persamaan kuadrat pada umumnya. Pangkat tertinggi pada pertidaksamaan kuadrat adalah 2 (dua). Perbedaan antara persamaan kuadrat dan pertidaksamaan kuadrat hanya terletak pada tanda penghubungnya. Untuk lebih jelasnya, perhatikan contoh perbedaan antara persamaan kuadrat dan pertidaksamaan kuadrat yang diberikan melalui tabel di bawah.

Menentukan Akar-Akar Pertidaksamaan Kuadrat
Langkah pertama untuk menentukan himpunan penyelesaian pertidaksamaan kuadrat adalah menentukan akar-akar pertidaksamaan kuadrat. Pada bagian awal telah disinggung bahwa cara menentukan akar-akar pertidaksamaan kuadrat sama dengan cara menentukan akar-akar persamaan kuadrat. Perbedaannya hanya dengan mengambil harga nol dari soal pertidaksamaan kuadrat yang diberikan.
Cara mengambil nilai nol dari pertidaksamaan kuadrat hanya dengan cara mengganti tanda pertidaksamaan menjadi tanda sama dengan. Sehingga diperoleh bentuk sementara berupa persamaan kuadrat. Sebagai contoh, perhatikan cara mengambil harga nol dari pertidaksamaan berikut ini.

Cara yang sama juga berlaku untuk semua tanda pertidaksamaan.
Dengan mengambil nilai nol, sobat idschool akan mendapatkan persamaan kuadrat. Selanjutnya, cari akar-akar yang memenuhi persamaan kuadrat tersebut. Cara menentukan akar-akar persamaan kuadrat dapat menggunakan metode pemfaktoran, rumus abc, atau metode melengkapkan kuadrat sempurna.

Setelah mendapatkan akar-akar persamaan kuadrat yang memenuhi. Buatlah garis bilangan dan menentukan nilai pada masing-masing daerah. Nilai yang dimaksud di sini dapat berupa nilai positif (+) atau negatif .
Simak ulasan lebih lengkap mengenai garis bilangan dan cara menentukan tanda pada masing-masing daerah pada pembahasan dibawah.
Garis Bilangan dan Cara Menentukan Tanda pada Masing-Masing Daerah
Misalkan nilai akar-akar yang diperoleh dari perhitungan sebelumnya adalah a dan b. Maka garis bilangan yang dapat dibentuk dapat dilihat seperti gambar di bawah.

Setelah dapat membentuk daerah garis bilangan seperti pada gambar di atas, berikutnya adalah menentukan nilai pada masing-masing daerah. Caranya adalah dengan mengambil satu titik uji pada suatu daerah.
TIPS: untuk mempermudah perhitungan ambil titik uji x = 0.
Hasil dari titik uji menunjukkan nilai yang mewakili keseluruhan daerah tersebut. Untuk daerah yang lain, biasanya akan bergantian. Maksudnya, jika hasil titik uji menghasilkan daerah positif maka daerah sebelahnya adalah kebalikannya. Begitu juga dengan kondisi sebaliknya.

Namun terdapat pengecualian ketika ada akar kembar hasil dari penentukan akar-akar persamaan kuadrat. Tandanya mengikuti daerah sebelahnya. Perhatikan ilustrasi pada gambar di bawah.

Bagaimana, sudah paham? Cara menentukan tanda pada daerah di garis bilangan akan membantu sobat idschool untuk menentukanhimpunan penyelesaian pertidaksamaan kuadrat. Perhatikan cara menggunakannya pada bagian contoh soal dan pembahasan himpunan penyelesaian pertidaksamaan kuadrat. Sebelumnya, akan diulas terlebih dahulu cara membentuk himpunan penyelesaian yang disajikan dalam garis bilangan ke dalam persamaan himpunan. Simak ulasannya di bawah.
Himpunan Penyelesaian Pertidaksamaan Kuadrat
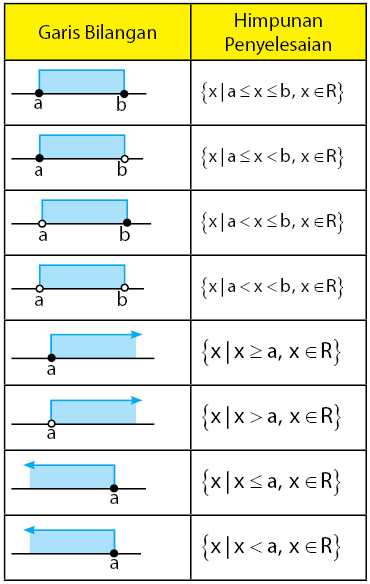
Hasil dari daerah yang memenuhi pertidaksamaan kuadrat biasanya disajikan dalam bentuk himpunan. Pada bagian ini, sobat idschool akan mempelajari cara menentukan notasi himpunan dari garis bilangan. Berikut ini adalah tabel cara membaca himpunan penyelesaian dari garis bilangan yang diberikan secara umum.
Untuk menambah pemahaman sobat idschool terkait materi pertidaksamaan kuadrat. Berikut ini akan diberikan dua contoh soal cara menentukan himpunan penyelesaian pada pertidaksamaan kuadrat beserta dengan pembahasannya.
Contoh Soal dan Pembahasan
Contoh 1: Soal Pertidaksamaan Kuadrat
Himpunan penyelesaian yang memenuhi pertidaksamaan kuadrat
![\[ x^{2} - x - 12 \leq 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-055097ae678ffbac5b49cf1cca6a0804_l3.png)
adalah ….
![\[ \textrm{A.} \; \; \; \left \{ x \leq -3 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-86ea573e1b6e2bf80d0de075b0da329b_l3.png)
![\[ \textrm{B.} \; \; \; \left \{ x \leq 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3976159b037f7f81fd34adba247185f7_l3.png)
![\[ \textrm{C.} \; \; \; \left \{ x \leq -3 \; \textrm{atau} \; x \geq 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-55547e65242ef08fe791ef133918b17d_l3.png)
![\[ \textrm{D.} \; \; \; \left \{ x \leq -3 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-fa23b28bb0e561ec5b0fa37db95c4339_l3.png)
![\[ \textrm{E.} \; \; \; \left \{ -3 \leq x \leq 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-15015ffb19b061bfea8c3474bab89f1e_l3.png)
Pembahasan:


Harga nol dari pertidaaksamaan kuadrat adalah . Selanjutnya akan ditentukan akar-akar persamaan kuadrat yang memenuhi.
![\[ x^{2} - x - 12 = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-ca5aacd599784bc12537a5d24464ce65_l3.png)
![\[ \left(x + 3 \right) \left(x - 4 \right) = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-54a0fa9f47bb8a0a585322a61199c050_l3.png)
![\[ \left(x + 3 \right) = 0 \; \textrm{atau} \; \left(x - 4 \right) = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-7b93f78cfc34732596f35c282e72e5dd_l3.png)
![\[ x = - 3 \; \textrm{atau} \; x = 4 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-2e8bae4e9b996695f2d3c16ec6aac2e6_l3.png)
Baca Juga: pemfaktoran bentuk aljabar untuk menentukan akar-akar persamaan kuadrat
Sehingga dapat diperoleh daerah pada garis bilangan dengan batas seperti gambar di bawah.

Selanjutnya, akan diselidiki nilai dari masing-masing daerah.
Ambil titik uji x = 0, kemudian substitusikan nilainya ke persamaan kuadrat
![\[ 0^{2} - 0 - 12 = -12 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-391fdd15c873d349077f63ca3c539206_l3.png)
Untuk x = 0 menghasilkan nilai negatif, sehingga daerah yang memuat angka nol, daerahnya adalah negatif.
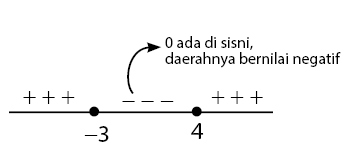

Pertidaksamaan kuadrat yang diberikan adalah , artinya himpunan penyelesaian dipenuhi untuk daerah yang bernilai positif.

Jadi himpunan penyelesaiannya adalah
![\[ \left \{ x \leq -3 \; \textrm{atau} \; x \geq 4 \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-1746b740845222d12c34925aefabb7c6_l3.png)
Jawaban: C
Contoh 2: Soal Pertidaksamaan Kuadrat
Himpunanan penyelesaian dari pertidaksamaan
![\[ x^{2} - 5x - 14 \leq 0, x \in R \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3db2403268ab665be7b24ea92d34b28f_l3.png)
adalah ….
![\[ \textrm{E.} \; \; \; \left \{ x \; | \; -2 \leq x \leq 7, \; x \in R \right \} \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-babba9f2588c35e3b1a725673e599b69_l3.png)
Pembahasan:


Harga nol sari adalah . Selanjutnya akan dicari akar-akar persamaan kuadrat tersebut.
![\[ x^{2} - 5x - 14 = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-16d292fb7d697a5b33233e41726e1693_l3.png)
![\[ \left( x - 7 \right) \left(x + 2 \right) = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d185e602519c2b8edcefd3aa7495609e_l3.png)
Sehingga diperoleh
![\[ \left( x - 7 \right) = 0 \; \textrm{atau} \left(x + 2 \right) = 0 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-96b85b6414512d94ca94400830155f7b_l3.png)
![\[ x = 7 \; \textrm{atau} \; x = - 2 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-3e451d90aa7e46fc125ad037e52938fa_l3.png)
Berdasarkan hasil di atas, dapat dibentuk batas daerah dalam garis bilangan seperti gambar di bawah.

Selanjutnya, akan diselidiki nilai dari masing-masing daerah.
Ambil titik uji x = 0, kemudian substitusikan nilainya ke persamaan kuadrat
![\[ 0^{2} - 5 \times 0 - 14 = -14 \]](https://idschool.net/wp-content/ql-cache/quicklatex.com-d92cf00d5bfddbd939c1fc4a9192fc4c_l3.png)
Untuk x = 0 menghasilkan nilai negatif, sehingga daerah yang memuat angka nol, daerahnya adalah negatif.
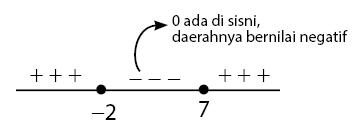

Pertidaksamaan kuadrat yang diberikan adalah , artinya himpunan penyelesaian dipenuhi untuk daerah yang bernilai negatif.

Jadi himpunan penyelesaiannya adalah .
Jawaban: E
Contoh 3
x(3x + 1) < (x + 1)² − 1
Penyelesaian :
Terlebih dahulu ubah ke dalam bentuk umum pertidaksamaan kuadrat :
x(3x + 1) < (x + 1)² − 1
⇔ 3x² + x < x² + 2x + 1 − 1
⇔ 2x² − x < 0
Pembuat nol :
2x² − x = 0
x(2x − 1) = 0
x = 0 atau x = 1212
Untuk interval x > 1212 ambil x = 1
2x² − x = 2(1)² − 1 = 1 (+)

Karena pertidaksamaan bertanda “<” , maka daerah penyelesaian berada pada interval yang bertanda (−).
∴ HP = {0 < x < 1212}
Perhatikan grafik fungsi kuadrat berikut :
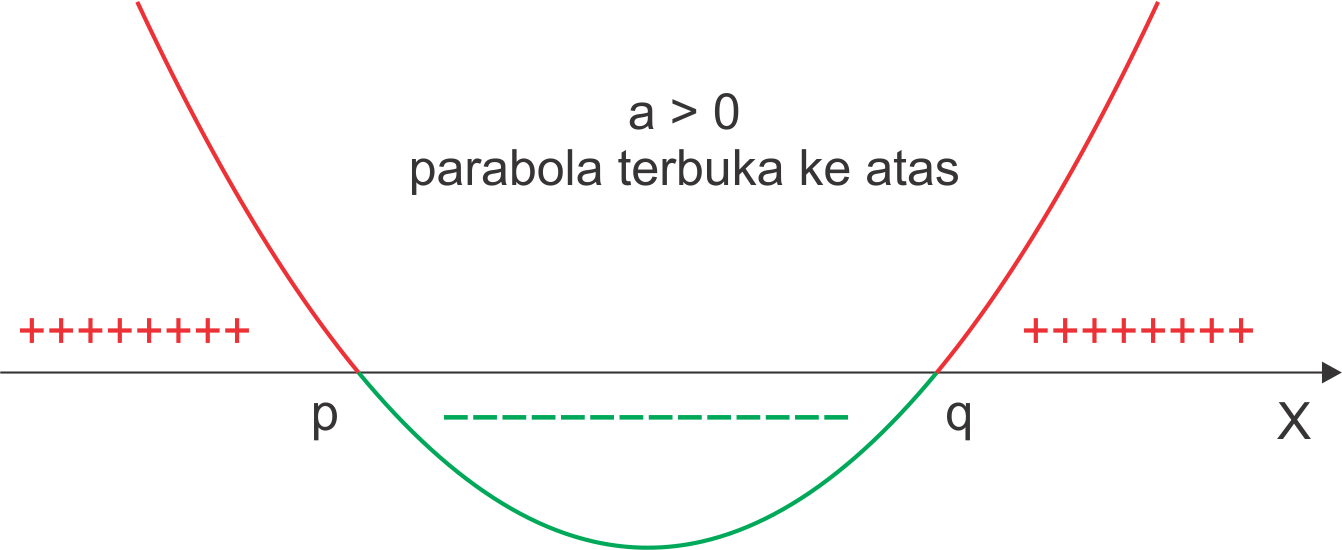
Dari grafik diatas dapat dilihat bahwa :
Untuk interval x < p atau x > q kurvanya berada diatas sumbu-x sehingga nilai fungsi pada interval tersebut bernilai positif (> 0)
Untuk interval p < x < q kurvanya berada dibawah sumbu-x sehingga nilai fungsi pada interval tersebut bernilai negatif (< 0)
Berdasarkan uraian diatas, himpunan penyelesaian suatu pertidaksamaan kuadrat dapat pula ditentukan dengan konsep berikut :
Misalkan pembuat nol suatu pertidaksamaan kuadrat dengan a > 0 adalah p dan q. Untuk p < q, berlaku :
- Jika pertidaksamaan bertanda “>”, makaHP={x<pataux>q}HP={x<pataux>q}
- Jika pertidaksamaan bertanda “<“, makaHP={p<x<q}HP={p<x<q}
Perlu diperhatikan bahwa konsep diatas berlaku untuk a > 0. Jika a bernilai negatif, maka terlebih dahulu kalikan kedua ruas dengan negatif (−).
Dengan menggunakan konsep diatas, contoh-contoh sebelumnya dapat diselesaikan dengan cara sebagai berikut.
(1) x² − 2x − 3 ≥ 0
Pembuat nol :
x² − 2x − 3 = 0
(x + 1)(x − 3) = 0
x = −1 atau x = 3
Karena pertidaksamaan bertanda “≥”, maka
HP = {x ≤ −1 atau x ≥ 3}
(2) −x² − 3x + 4 > 0
Kalikan kedua ruas dengan (−) :
x² + 3x − 4 < 0
Pembuat nol :
x² + 3x − 4 = 0
(x + 4)(x − 1) = 0
x = −4 atau x = 1
Karena pertidaksamaan bertanda “<“, maka
HP = {−4 < x < 1}
(3) 2x² − x < 0
Pembuat nol :
2x² − x = 0
x(2x − 1) = 0
x = 0 atau x = 1212
Karena pertidaksamaan bertanda “<“, maka
HP = {0 < x < 1212}
4. Himpunan penyelesaian dari pertidaksamaan 2×2 + 5x + 15 < 3×2 + 5x – 1, untuk x ɛR adalah:
a. {x|x < 4 atau x > 4, ɛR}
b. {x|x < -4 atau x > 4, ɛR}
c. {x|x < -4 atau x > 1, ɛR}
d. {x|x -4 < x > 1, ɛR}
e. {x|x -4 ≤ x > 1, ɛR}
Jawab: b. {x|x < -4 atau x > 4, ɛR}
Pembahasan:
2×2 + 5x + 15 < 3×2 + 5x – 1
2×2 + 5x + 15 – 3×2 – 5x + 1 < 0
-x2 + 16 < 0
x2 – 16 > 0
pembuat nol:
(x – 4)(x + 4) = 0
x = 4 atau x = -4
ambil x = 0
x2 – 16 = 02 – 16 = -16 (negatif)
+ – +
-2 7
Jadi himpunan penyelesaian adalah:
{x|x < -4 atau x > 4, ɛR}
5. Penyelesaian pertidaksamaan 3×2 – 13x – 10 > 0 adalah:
a. x < atau x > 10
b. x < atau x >
c. x < atau x > 5
d. < x < 5
e. < x < 10
Jawab: c. x < atau x > 5
Pembahasan:
3×2 – 13x – 10 > 0
(3x + 2)(x – 5) > 0
x < atau x > 5
6. Himpunan penyelesaian pertidaksamaan 3×2 – 2x – 8 > 0, untuk x ɛ R adalah:
a. {x|x > 5 atau x < }
b. {x|x > 2 atau x < }
c. {x|x > atau x < 2 }
d. {x| < x < 2 }
e. {x| < x < 2 }
Jawab: b. {x|x > 2 atau x < }
Pembahasan:
3×2 – 2x – 8 > 0
(3x + 4)(x – 2) > 0 (positif)
x = 2
+ – +
2
Jadi Hp = {x|x > 2 atau x < }
7. Himpunan penyelesaian dari 24 + 5x – x2 ≤ 0 adalah:
a. {x|x ≤ -3 atau x ≥ 8}
b. {x|x ≤ -3 atau x ≥ -8}
c. {x|x ≤ 3 atau x ≥ 8}
d. {x|x ≤ 1/3 atau x ≥ 8}
e. {x|x ≤ -1/3 atau x ≥ 8}
Jawab: a. {x|x ≤ -3 atau x ≥ 8}
Pembahasan :
24 + 5x – x2 ≤ 0
x2 – 5x – 24 ≥ 0
(x + 3)(x – 8) ≥ 0
X ≤ -3 atau x ≥ 8
8. Himpunan penyelesaian pertidaksamaan (x + 1)(2x + 3) ≥ 1 adalah:
a. {x|x ≤ -1/2 atau c ≥ 2}
b. {x|x ≤ -2 atau c ≥ -1/2}
c. {x|-2 ≤ atau c ≥ -1/2}
d. {x|-2 ≤ x ≤ -1/2}
e. {x|-1/2 ≤ x ≤ 2}
Jawab: b. {x|x ≤ -2 atau c ≥ -1/2}
Pembahasan:
(x + 1)(2x + 3) ≥ 1
x = – ½ x = -2
+ – +
-2 -½
Jadi Hp = {x|x ≤ -2 atau c ≥ -1/2}
9. Himpunan penyelesaian pertidaksaman 2(x + 1)2 < 3×2 + 6(x – 1) adalah:
a. {x|-4 < x < 2, x ɛ R}
b. {x|-2 < x < 4, x ɛ R}
c. {x|2 < x < 4, x ɛ R}
d. {x|x < -4 atau x > 2, x ɛ R}
e. {x|x < -2 atau x > 4, x ɛ R}
Jawab: d. {x|x < -4 atau x > 2, x ɛ R}
Pembahasan:
2(x + 1)2 < 3×2 + 6(x – 1)
2(x2 + 2x + 1) < 3×2 + 6x – 6
2×2 + 4x + 2 < 3×2 + 6x – 6
– x2 – 2x + 8 <0
x2 + 2x – 8 > 0
(x + 4)(x – 2) > 0
x < – 4 atau x > 2
10. Himpunan penyelesaian pertidaksamaan –2×2 – 5x + 3 ≤ 0, x ɛ R adalah:
a. {x|x ≤ -3 atau x ≥ ½}
b. {x|x ≤ -½ atau x ≥ 3}
c. {x|-3 ≤ x atau x ≥ ½}
d. {x|½ ≤ x ≥ 3}
e. {x|x ≤ -3 atau x ≥ -½}
Jawab: a. {x|x ≤ -3 atau x ≥ ½}
Pembahasan:
–2×2 – 5x + 3 ≤ 0 (dikalikan – 1)
2×2 + 5x – 3 ≥ 0
(2x – 1)(x + 3) ≥ 0 (positif)
Pembuat nol adalah
(2x – 1)(x + 3) = 0
x = ½ x = -3
+ – +
-3 ½
Jadi, Hp = {x|x ≤ -3 atau x ≥ ½}
Demikianlah tadi ulasan materi tentang pertidaksamaan kaudrat. Meliputi bentuk umum pertidaksamaan kuadrart sampai dengan cara menentukan himpunan penyelesaian pertidaksamaan kuadrat.
Sumber :
https://syaqila.net/matematika/soal-pertidaksamaan-kuadrat-dan-pembahasannya.html
https://idschool.net/sma/pertidaksamaan-kuadrat-dan-himpunan-penyelesaiannya/